SageMathとグラフ理論（平面グラフ）

問題12.1
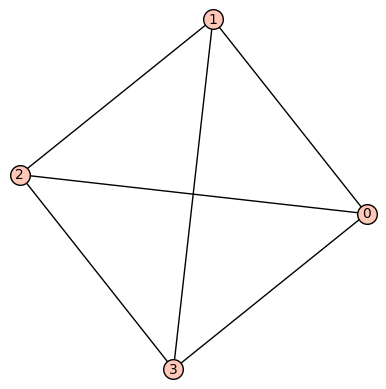
(i) 頂点数5の車輪Wheel、が平面グラフであることをグラフで示せ。
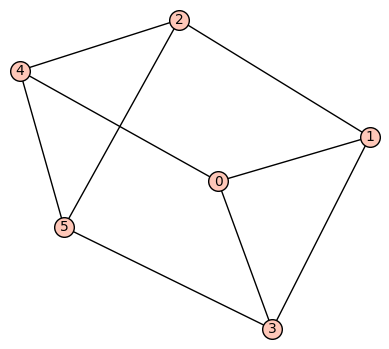
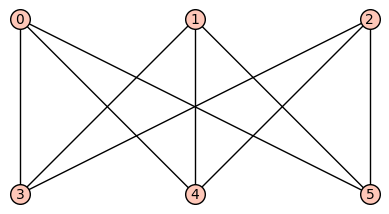
(ii) octahedron(八面体)が平面グラフであることをグラフで示せ。

すなおに描くと平面グラフになってしまう。

問題の意図としては必ずしも平面グラフでないものを平面グラフ的(planar)に描けということなのでしょうが、SageMathは自動的になるべく平面的に描いてしまう。頂点の場所を指定する方法があるだろうけどまだ調べられていません。

# planar01.sage
# attach('planar01.sage')

Gw5=graphs.WheelGraph(5)
p1=plot(Gw5)
Go=graphs.OctahedralGraph()
p2=plot(Go)
# graphics_array([p1,p2])

追記: こんなことができました。

頂点の配置に、'spring'というのと'circular'というのを指定すると、0を中心に配置するのと、すべての点を円周上に配置するのが選べます。

Gw5.graphplot(save_pos=True, layout='spring')
p3=plot(Gw5)
Gw5.graphplot(save_pos=True, layout='circular')
p4=plot(Gw5)
Go.graphplot(save_pos=True, layout='spring')
p5=plot(Go)
Go.graphplot(save_pos=True, layout='circular')
p6=plot(Go)
graphics_array([p3,p4,p5,p6],2,2)

SageMathでグラフ理論(クラトウスキーの定理）

THEOREM 12.2(Kuratowski, 1930). A graph is planar if and only if it contains no subgraph homeomorphic to or .

グラフが平面グラフであるための必要十分条件はが またはと位相同型な部分グラフを含まないことである。

THEOREM 12.3 A graph is planar if and only if it contains no subgraph contractible to or .

contractibleというのは、頂点を重ねること(縮約)によって頂点と辺の数をへらしていくことで、例として、Petersenグラフの内側の5つの点を外側に重ね合わせると次のようになります。

# pertsen.sage

G=graphs.PetersenGraph()
p1=plot(G)

G2=copy(G)

G2.merge_vertices([0,5])
G2.merge_vertices([1,6])
G2.merge_vertices([2,7])
G2.merge_vertices([3,8])
G2.merge_vertices([4,9])
p2=plot(G2)
# graphics_array( (p1,p2))

SageMathとグラフ理論（次数の数列とグラフ的について）

次数(degree)の数列を与えられて単純グラフ（ループや多重辺がないグラフ）が描けるかどうか（グラフ的）かどうかを問う問題があります。

例えば[3,3,3,3,3,3]だと3点と3点の完全二部グラフが描けますのでグラフ的である、という解答が載っていたりする。

しかしこれはたまたま解けただけであって、完全二部グラフ以外に[3,3,3,3,3,3]のグラフがあるかどうかもわからないし、そもそも思いつかなかったら描けないことをどう証明するのか。

と思ったりして、次数を与えて、グラフが描けるかどうかを調べる関数を探してみたらありました。

G=graphs.DegreeSequence([3,3,3,3])
show(G)

G=graphs.DegreeSequence([3,3,3,4])
-> invalid degree sequence

[3,3,3,4]ではグラフが描けないので、エラーになります。つまり、[3,3,3,4]はグラフ的ではない。

次に[3,3,3,3,3,3]の場合。

G=graphs.DegreeSequence([3,3,3,3,3,3])
show(G)

で描けたのはいいのですが、完全二部グラフではない。完全二部グラフだと次のようになります。

G2=graphs.CompleteBipartiteGraph(3,3)
show(G2)

グラフ的かどうかは解けたけど、今度は別の問題が生じてしまいました。

いくつ書けるのか。同じものなのか。

G==G2
False
G.is_isomorphic(G2)
False

ちがうらしい。同型ではない。

G=graphs.DegreeSequence([3,3,3,3,3,3])

では描けるものを描くだけで、他にもグラフがあるかどうかは示してくれないようなので、他の方法を考える必要があります。

list(G.degree_iterator())
[3, 3, 3, 3, 3, 3]

とすると、次数の数列にしてくれるので、6頂点のグラフすべての次数の数列を作って、これと同じグラフがいくつあるかしらべるのがいいと思う。めんどくさそうだけど、ちょっと試行錯誤してみます。

Glist=filter (lambda G: G.is_connected(), graphs(6))
len(Glist)
112

うむ。連結グラフだけで112個もある。

しかし一応この112個は同型ではないはずなので、これを順々にフィルターにかけていく。

Glist2 = map (lambda G: G.degree_iterator(), Glist)
Glist3 = map (list , Glist2)
Glist4 = filter (lambda L: L == [3,3,3,3,3,3], Glist3)
len(Glist4)
2

Glist2で次数を数えて、Glist3でそれをリストにして、Glist4で[3,3,3,3,3,3]のものを抜いて、要素数を数えると2個だったので、[3,3,3,3,3,3]のラベル無しのグラフは2種類しかないことが確認できたと思います。

うむ。このやり方では数しかわからないけど、まあ、今日はここまで。

SageMathとグラフ理論（接続行列incidence matrix)

接続行列からでもグラフがかけるか実験します。

接続行列Mで与えられるグラフを描け。

M=matrix(5,8,[[0,0,1,1,1,1,1,0],[0,1,0,1,0,0,0,1],[0,0,0,0,0,0,0,1],[1,0,1,0,1,0,1,0],[1,1,0,0,0,1,0,0]])

G=Graph(M)
show(G)

描けました。

ということは、接続行列と隣接行列(adjacent matrix)の相互変換が可能ということか。

sage: G.incidence_matrix()
[1 1 1 1 1 0 0 0]
[1 0 0 0 0 1 1 0]
[0 0 0 0 0 1 0 0]
[0 1 1 1 0 0 0 1]
[0 0 0 0 1 0 1 1]

sage: G.adjacency_matrix()
[0 1 0 3 1]
[1 0 1 0 1]
[0 1 0 0 0]
[3 0 0 0 1]
[1 1 0 1 0]

できました。便利かも。

SageMathとグラフ理論（連結グラフ）

introduction to graph theory by wilsonのp.11のFig.2.9は頂点が5個までの連結グラフ(connected unlabelled graph)で、31個ある。

これを作る。

（なぜならテキストの練習問題で何度も使われるから。例えば、この内、ツリーはどれとどれか。とか。）

sage: len (filter (lambda G: G.is_connected(), list(graphs(1)) + list(graphs(2))
....: + list(graphs(3)) + list(graphs(4)) + list(graphs(5))))
31

数は合っているみたいなので、これからグラフを描いてみる。

sage: glist = filter (lambda G: G.is_connected(), list(graphs(1)) + list(graphs(
....: 2)) + list(graphs(3)) + list(graphs(4)) + list(graphs(5)))
sage: p0=plot(Graph(0))
sage: gplotlist = map (plot, glist)
sage: graphics_array( (gplotlist + [p0]*4), 7, 5)

こうしておけば、この内ツリーはどれとどれかというのは次のように解けます。

sage: len(filter (lambda G: G.is_tree(), glist))
8

sage: glist2=filter (lambda G: G.is_tree(), glist)
sage: gplotlist2= map(plot, glist2)
sage: graphics_array(gplotlist2, 2)

SageMathとグラフ理論（隣接行列、接続行列、ラプラシアン（キルヒホフ）行列）

まず、ひとつグラフを作ります。

V=['P','Q','R','S','T']
E=[['P','Q'],['Q','R'],['R','S'],['S','T'],['T','P'],['P','S'],['Q','T'],['Q','S']]
g=Graph([V,E])

隣接行列

sage: g.adjacency_matrix()
[0 1 0 1 1]
[1 0 1 1 1]
[0 1 0 1 0]
[1 1 1 0 1]
[1 1 0 1 0]

接続行列
sage: g.incidence_matrix()
[1 0 0 0 1 1 0 0]
[1 1 1 1 0 0 0 0]
[0 0 1 0 0 0 1 0]
[0 1 0 0 1 0 1 1]
[0 0 0 1 0 1 0 1]

ラプラシアン行列

sage: g.laplacian_matrix()
[ 3 -1 0 -1 -1]
[-1 4 -1 -1 -1]
[ 0 -1 2 -1 0]
[-1 -1 -1 4 -1]
[-1 -1 0 -1 3]

キルヒホフ行列

sage: g.kirchhoff_matrix()
[ 3 -1 0 -1 -1]
[-1 4 -1 -1 -1]
[ 0 -1 2 -1 0]
[-1 -1 -1 4 -1]
[-1 -1 0 -1 3]

ヘルプによると、ラプラシアン行列とキルヒホフ行列は同じものだそうです。

SageMathとグラフ理論（カノニカル行列）

Pythonのdictionaryの形で次のように指定すると、グラフが描けます。

g1=Graph({'P':['Q','S','T'],'Q':['R','S','T'],'R':['S'],'S':['T']})
show(g1)

これはうまい具合に横向きになったし、なによりも頂点がアルファベット順ですがいつも必ずしもそうではありません。

ただし、隣接行列の形は常に一緒です。

g1.adjacency_matrix()
[0 1 0 1 1]
[1 0 1 1 1]
[0 1 0 1 0]
[1 1 1 0 1]
[1 1 0 1 0]

たぶん人間には一番わかり易い頂点のリストと辺のリストを組み合わせた指定の仕方をしてみます。

V=['P','Q','R','S','T']
E=[['P','Q'],['Q','R'],['R','S'],['S','T'],['T','P'],['P','S'],['Q','T'],['Q','S']]
g2=Graph([V,E])
show(g2)

g2.adjacency_matrix()
[0 1 0 1 1]
[1 0 1 1 1]
[0 1 0 1 0]
[1 1 1 0 1]
[1 1 0 1 0]

行列の形が同じになりましたが、これは偶然かもしれない。

カノニカルラベルに振りなおしてみます。

(g1.canonical_label()).adjacency_matrix()
[0 0 0 1 1]
[0 0 1 1 1]
[0 1 0 1 1]
[1 1 1 0 1]
[1 1 1 1 0]

今度は行列の形は違いますが、同じもののはずです。

g3=Graph( (g1.canonical_label()).adjacency_matrix())
show(g3)

g1.is_isomorphic(g3)
True
g2.is_isomorphic(g3)
True

ほらね。