SageMathでグラフに関係してどんな関数があるか、とか調べるときにタブ補完(Tab completion)を使います。
たとえば、グラフを書きたいとき、
G=graphs.<TAB>
と押すと、200個ほどの関数がある。
また、G=Graph()としたうえで、
G.<TAB>
と押すと、グラフに使える関数が300個以上あります。
これが一覧性がなくて、マニュアルに一覧表もないようなので、コピペで作ってみました。
参考のために作り方ですが、端末(ターミナル)をできるだけ上下左右に大きくとります。端末の範囲内で一覧表示をするので、clearしたうえで<TAB>を使えばたいていの場合、一覧できると思います。今回のように数百あって、何ページかにまたがる場合は、テキストエディターにコピペして、ソートして、コピペの際に生じた重複を消すなどの作業をします。私の場合、Haskellでやりました。
contents <- readFile "graphs_tab.txt"
writeFile "graphs_tab02.txt" $ unlines $ nub $ sort $ words contents
みたいな感じ。
さて、G=graphs.<TAB>の結果とG.<TAB>の結果です。
graphs.AffineOrthogonalPolarGraph
graphs.AhrensSzekeresGeneralizedQuadrangleGraph
graphs.Balaban10Cage
graphs.Balaban11Cage
graphs.BalancedTree
graphs.BarbellGraph
graphs.BidiakisCube
graphs.BiggsSmithGraph
graphs.BishopGraph
graphs.BlanusaFirstSnarkGraph
graphs.BlanusaSecondSnarkGraph
graphs.BrinkmannGraph
graphs.BrouwerHaemersGraph
graphs.BubbleSortGraph
graphs.BuckyBall
graphs.BullGraph
graphs.ButterflyGraph
graphs.CameronGraph
graphs.Cell120
graphs.Cell600
graphs.ChessboardGraphGenerator
graphs.ChvatalGraph
graphs.CirculantGraph
graphs.CircularLadderGraph
graphs.ClawGraph
graphs.ClebschGraph
graphs.CompleteBipartiteGraph
graphs.CompleteGraph
graphs.CompleteMultipartiteGraph
graphs.CossidentePenttilaGraph
graphs.CoxeterGraph
graphs.CubeGraph
graphs.CycleGraph
graphs.DegreeSequence
graphs.DegreeSequenceBipartite
graphs.DegreeSequenceConfigurationModel
graphs.DegreeSequenceExpected
graphs.DegreeSequenceTree
graphs.DejterGraph
graphs.DesarguesGraph
graphs.DiamondGraph
graphs.DodecahedralGraph
graphs.DorogovtsevGoltsevMendesGraph
graphs.DoubleStarSnark
graphs.DurerGraph
graphs.DyckGraph
graphs.EllinghamHorton54Graph
graphs.EllinghamHorton78Graph
graphs.EmptyGraph
graphs.ErreraGraph
graphs.F26AGraph
graphs.FibonacciTree
graphs.FlowerSnark
graphs.FoldedCubeGraph
graphs.FolkmanGraph
graphs.FosterGraph
graphs.FranklinGraph
graphs.FriendshipGraph
graphs.FruchtGraph
graphs.FuzzyBallGraph
graphs.GeneralizedPetersenGraph
graphs.GoethalsSeidelGraph
graphs.GoldnerHararyGraph
graphs.GossetGraph
graphs.GrayGraph
graphs.Grid2dGraph
graphs.GridGraph
graphs.GrotzschGraph
graphs.HaemersGraph
graphs.HallJankoGraph
graphs.HanoiTowerGraph
graphs.HararyGraph
graphs.HarborthGraph
graphs.HarriesGraph
graphs.HarriesWongGraph
graphs.HeawoodGraph
graphs.HerschelGraph
graphs.HexahedralGraph
graphs.HigmanSimsGraph
graphs.HoffmanGraph
graphs.HoffmanSingletonGraph
graphs.HoltGraph
graphs.HortonGraph
graphs.HouseGraph
graphs.HouseXGraph
graphs.HyperStarGraph
graphs.IcosahedralGraph
graphs.IntersectionGraph
graphs.IntervalGraph
graphs.IoninKharaghani765Graph
graphs.JankoKharaghaniGraph
graphs.JankoKharaghaniTonchevGraph
graphs.JohnsonGraph
graphs.KingGraph
graphs.KittellGraph
graphs.Klein3RegularGraph
graphs.Klein7RegularGraph
graphs.KneserGraph
graphs.KnightGraph
graphs.KrackhardtKiteGraph
graphs.LCFGraph
graphs.LadderGraph
graphs.LivingstoneGraph
graphs.LjubljanaGraph
graphs.LocalMcLaughlinGraph
graphs.LollipopGraph
graphs.M22Graph
graphs.MarkstroemGraph
graphs.MathonPseudocyclicMergingGraph
graphs.MathonPseudocyclicStronglyRegularGraph
graphs.MathonStronglyRegularGraph
graphs.McGeeGraph
graphs.McLaughlinGraph
graphs.MeredithGraph
graphs.MoebiusKantorGraph
graphs.MoserSpindle
graphs.MuzychukS6Graph
graphs.MycielskiGraph
graphs.MycielskiStep
graphs.NKStarGraph
graphs.NStarGraph
graphs.NauruGraph
graphs.NonisotropicOrthogonalPolarGraph
graphs.NonisotropicUnitaryPolarGraph
graphs.OctahedralGraph
graphs.OddGraph
graphs.OrthogonalArrayBlockGraph
graphs.OrthogonalPolarGraph
graphs.PaleyGraph
graphs.PappusGraph
graphs.PasechnikGraph
graphs.PathGraph
graphs.PerkelGraph
graphs.PermutationGraph
graphs.PetersenGraph
graphs.PoussinGraph
graphs.QueenGraph
graphs.RandomBarabasiAlbert
graphs.RandomBipartite
graphs.RandomBoundedToleranceGraph
graphs.RandomGNM
graphs.RandomGNP
graphs.RandomHolmeKim
graphs.RandomIntervalGraph
graphs.RandomLobster
graphs.RandomNewmanWattsStrogatz
graphs.RandomRegular
graphs.RandomShell
graphs.RandomToleranceGraph
graphs.RandomTree
graphs.RandomTreePowerlaw
graphs.RandomTriangulation
graphs.RingedTree
graphs.RobertsonGraph
graphs.RookGraph
graphs.SchlaefliGraph
graphs.ShrikhandeGraph
graphs.SierpinskiGasketGraph
graphs.SimsGewirtzGraph
graphs.SousselierGraph
graphs.SquaredSkewHadamardMatrixGraph
graphs.StarGraph
graphs.SuzukiGraph
graphs.SwitchedSquaredSkewHadamardMatrixGraph
graphs.SylvesterGraph
graphs.SymplecticDualPolarGraph
graphs.SymplecticGraph
graphs.SymplecticPolarGraph
graphs.SzekeresSnarkGraph
graphs.T2starGeneralizedQuadrangleGraph
graphs.TaylorTwographDescendantSRG
graphs.TaylorTwographSRG
graphs.TetrahedralGraph
graphs.ThomsenGraph
graphs.TietzeGraph
graphs.ToleranceGraph
graphs.Toroidal6RegularGrid2dGraph
graphs.ToroidalGrid2dGraph
graphs.TruncatedIcosidodecahedralGraph
graphs.TruncatedTetrahedralGraph
graphs.TuranGraph
graphs.Tutte12Cage
graphs.TutteCoxeterGraph
graphs.TutteGraph
graphs.UnitaryDualPolarGraph
graphs.UnitaryPolarGraph
graphs.WagnerGraph
graphs.WatkinsSnarkGraph
graphs.WellsGraph
graphs.WheelGraph
graphs.WienerArayaGraph
graphs.WorldMap
graphs.chang_graphs
graphs.cospectral_graphs
graphs.fullerenes
graphs.fusenes
graphs.line_graph_forbidden_subgraphs
graphs.nauty_geng
graphs.petersen_family
graphs.planar_graphs
graphs.quadrangulations
graphs.sage
graphs.strongly_regular_graph
graphs.trees
graphs.triangulations
G.add_cycle
G.add_edge
G.add_edges
G.add_path
G.add_vertex
G.add_vertices
G.adjacency_matrix
G.all_paths
G.allow_loops
G.allow_multiple_edges
G.allows_loops
G.allows_multiple_edges
G.am
G.antisymmetric
G.apex_vertices
G.automorphism_group
G.average_degree
G.average_distance
G.bipartite_color
G.bipartite_sets
G.blocks_and_cut_vertices
G.blocks_and_cuts_tree
G.bounded_outdegree_orientation
G.breadth_first_search
G.bridges
G.canonical_label
G.cartesian_product
G.categorical_product
G.category
G.center
G.centrality_betweenness
G.centrality_closeness
G.centrality_degree
G.characteristic_polynomial
G.charpoly
G.chromatic_number
G.chromatic_polynomial
G.chromatic_quasisymmetric_function
G.chromatic_symmetric_function
G.clear
G.clique_complex
G.clique_maximum
G.clique_number
G.clique_polynomial
G.cliques_containing_vertex
G.cliques_get_clique_bipartite
G.cliques_get_max_clique_graph
G.cliques_maximal
G.cliques_maximum
G.cliques_number_of
G.cliques_vertex_clique_number
G.cluster_transitivity
G.cluster_triangles
G.clustering_average
G.clustering_coeff
G.coarsest_equitable_refinement
G.coloring
G.complement
G.connected_component_containing_vertex
G.connected_components
G.connected_components_number
G.connected_components_sizes
G.connected_components_subgraphs
G.convexity_properties
G.copy
G.cores
G.cycle_basis
G.db
G.degree
G.degree_constrained_subgraph
G.degree_histogram
G.degree_iterator
G.degree_sequence
G.degree_to_cell
G.delete_edge
G.delete_edges
G.delete_multiedge
G.delete_vertex
G.delete_vertices
G.density
G.depth_first_search
G.diameter
G.disjoint_routed_paths
G.disjoint_union
G.disjunctive_product
G.distance
G.distance_all_pairs
G.distance_graph
G.distance_matrix
G.distances_distribution
G.dominating_set
G.dominator_tree
G.dump
G.dumps
G.eccentricity
G.edge_boundary
G.edge_connectivity
G.edge_cut
G.edge_disjoint_paths
G.edge_disjoint_spanning_trees
G.edge_iterator
G.edge_label
G.edge_labels
G.edges
G.edges_incident
G.eigenspaces
G.eigenvectors
G.eulerian_circuit
G.eulerian_orientation
G.export_to_file
G.faces
G.feedback_vertex_set
G.flow
G.fractional_chromatic_index
G.genus
G.get_embedding
G.get_pos
G.get_vertex
G.get_vertices
G.girth
G.gomory_hu_tree
G.graph6_string
G.graphics_array_defaults
G.graphplot
G.graphviz_string
G.graphviz_to_file_named
G.hamiltonian_cycle
G.has_edge
G.has_homomorphism_to
G.has_loops
G.has_multiple_edges
G.has_vertex
G.igraph_graph
G.ihara_zeta_function_inverse
G.incidence_matrix
G.independent_set
G.independent_set_of_representatives
G.is_apex
G.is_arc_transitive
G.is_asteroidal_triple_free
G.is_bipartite
G.is_cartesian_product
G.is_cayley
G.is_chordal
G.is_circulant
G.is_circular_planar
G.is_clique
G.is_connected
G.is_cut_edge
G.is_cut_vertex
G.is_directed
G.is_distance_regular
G.is_drawn_free_of_edge_crossings
G.is_edge_transitive
G.is_equitable
G.is_eulerian
G.is_even_hole_free
G.is_forest
G.is_gallai_tree
G.is_half_transitive
G.is_hamiltonian
G.is_immutable
G.is_independent_set
G.is_interval
G.is_isomorphic
G.is_line_graph
G.is_long_antihole_free
G.is_long_hole_free
G.is_odd_hole_free
G.is_overfull
G.is_partial_cube
G.is_perfect
G.is_planar
G.is_prime
G.is_regular
G.is_semi_symmetric
G.is_split
G.is_strongly_regular
G.is_subgraph
G.is_transitively_reduced
G.is_tree
G.is_triangle_free
G.is_vertex_transitive
G.is_weakly_chordal
G.join
G.kirchhoff_matrix
G.kirchhoff_symanzik_polynomial
G.kronecker_product
G.laplacian_matrix
G.latex_options
G.layout
G.layout_circular
G.layout_default
G.layout_extend_randomly
G.layout_graphviz
G.layout_planar
G.layout_ranked
G.layout_spring
G.layout_tree
G.lex_BFS
G.lexicographic_product
G.line_graph
G.longest_path
G.loop_edges
G.loop_vertices
G.loops
G.lovasz_theta
G.magnitude_function
G.matching
G.matching_polynomial
G.max_cut
G.maximum_average_degree
G.merge_vertices
G.min_spanning_tree
G.minimum_outdegree_orientation
G.minor
G.modular_decomposition
G.multicommodity_flow
G.multiple_edges
G.multiway_cut
G.name
G.neighbor_iterator
G.neighbors
G.networkx_graph
G.num_edges
G.num_faces
G.num_verts
G.number_of_loops
G.odd_girth
G.order
G.orientations
G.parent
G.perfect_matchings
G.periphery
G.plot
G.plot3d
G.radius
G.random_edge
G.random_edge_iterator
G.random_spanning_tree
G.random_subgraph
G.random_vertex
G.random_vertex_iterator
G.rank_decomposition
G.relabel
G.remove_loops
G.remove_multiple_edges
G.rename
G.reset_name
G.save
G.seidel_adjacency_matrix
G.seidel_switching
G.set_edge_label
G.set_embedding
G.set_latex_options
G.set_planar_positions
G.set_pos
G.set_vertex
G.set_vertices
G.shortest_path
G.shortest_path_all_pairs
G.shortest_path_length
G.shortest_path_lengths
G.shortest_paths
G.show
G.show3d
G.size
G.spanning_trees
G.spanning_trees_count
G.sparse6_string
G.spectral_radius
G.spectrum
G.steiner_tree
G.strong_orientation
G.strong_product
G.subdivide_edge
G.subdivide_edges
G.subgraph
G.subgraph_search
G.subgraph_search_count
G.subgraph_search_iterator
G.szeged_index
G.tensor_product
G.to_dictionary
G.to_directed
G.to_partition
G.to_simple
G.to_undirected
G.topological_minor
G.transitive_closure
G.transitive_reduction
G.traveling_salesman_problem
G.treewidth
G.triangles_count
G.tutte_polynomial
G.two_factor_petersen
G.twograph
G.union
G.vertex_boundary
G.vertex_connectivity
G.vertex_cover
G.vertex_cut
G.vertex_disjoint_paths
G.vertex_iterator
G.vertices
G.weighted
G.weighted_adjacency_matrix
G.wiener_index
G.write_to_eps
問題12.1
(i) 頂点数5の車輪Wheel、が平面グラフであることをグラフで示せ。
(ii) octahedron(八面体)が平面グラフであることをグラフで示せ。
すなおに描くと平面グラフになってしまう。
問題の意図としては必ずしも平面グラフでないものを平面グラフ的(planar)に描けということなのでしょうが、SageMathは自動的になるべく平面的に描いてしまう。頂点の場所を指定する方法があるだろうけどまだ調べられていません。
# planar01.sage
# attach('planar01.sage')
Gw5=graphs.WheelGraph(5)
p1=plot(Gw5)
Go=graphs.OctahedralGraph()
p2=plot(Go)
# graphics_array([p1,p2])
追記: こんなことができました。
頂点の配置に、'spring'というのと'circular'というのを指定すると、0を中心に配置するのと、すべての点を円周上に配置するのが選べます。
Gw5.graphplot(save_pos=True, layout='spring')
p3=plot(Gw5)
Gw5.graphplot(save_pos=True, layout='circular')
p4=plot(Gw5)
Go.graphplot(save_pos=True, layout='spring')
p5=plot(Go)
Go.graphplot(save_pos=True, layout='circular')
p6=plot(Go)
graphics_array([p3,p4,p5,p6],2,2)
THEOREM 12.2(Kuratowski, 1930). A graph is planar if and only if it contains no subgraph homeomorphic to or
.
グラフが平面グラフであるための必要十分条件は
が
または
と位相同型な部分グラフを含まないことである。
THEOREM 12.3 A graph is planar if and only if it contains no subgraph contractible to or
.
contractibleというのは、頂点を重ねること(縮約)によって頂点と辺の数をへらしていくことで、例として、Petersenグラフの内側の5つの点を外側に重ね合わせると次のようになります。
# pertsen.sage
G=graphs.PetersenGraph()
p1=plot(G)
G2=copy(G)
G2.merge_vertices([0,5])
G2.merge_vertices([1,6])
G2.merge_vertices([2,7])
G2.merge_vertices([3,8])
G2.merge_vertices([4,9])
p2=plot(G2)
# graphics_array( (p1,p2))
次数(degree)の数列を与えられて単純グラフ（ループや多重辺がないグラフ）が描けるかどうか（グラフ的）かどうかを問う問題があります。
例えば[3,3,3,3,3,3]だと3点と3点の完全二部グラフが描けますのでグラフ的である、という解答が載っていたりする。
しかしこれはたまたま解けただけであって、完全二部グラフ以外に[3,3,3,3,3,3]のグラフがあるかどうかもわからないし、そもそも思いつかなかったら描けないことをどう証明するのか。
と思ったりして、次数を与えて、グラフが描けるかどうかを調べる関数を探してみたらありました。
G=graphs.DegreeSequence([3,3,3,3])
show(G)
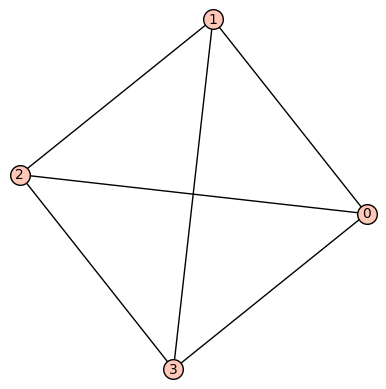
G=graphs.DegreeSequence([3,3,3,4])
-> invalid degree sequence
[3,3,3,4]ではグラフが描けないので、エラーになります。つまり、[3,3,3,4]はグラフ的ではない。
次に[3,3,3,3,3,3]の場合。
G=graphs.DegreeSequence([3,3,3,3,3,3])
show(G)
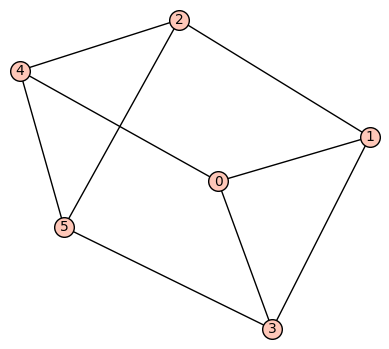
で描けたのはいいのですが、完全二部グラフではない。完全二部グラフだと次のようになります。
G2=graphs.CompleteBipartiteGraph(3,3)
show(G2)
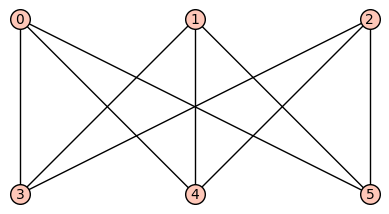
グラフ的かどうかは解けたけど、今度は別の問題が生じてしまいました。
いくつ書けるのか。同じものなのか。
G==G2
False
G.is_isomorphic(G2)
False
ちがうらしい。同型ではない。
G=graphs.DegreeSequence([3,3,3,3,3,3])
では描けるものを描くだけで、他にもグラフがあるかどうかは示してくれないようなので、他の方法を考える必要があります。
list(G.degree_iterator())
[3, 3, 3, 3, 3, 3]
とすると、次数の数列にしてくれるので、6頂点のグラフすべての次数の数列を作って、これと同じグラフがいくつあるかしらべるのがいいと思う。めんどくさそうだけど、ちょっと試行錯誤してみます。
Glist=filter (lambda G: G.is_connected(), graphs(6))
len(Glist)
112
うむ。連結グラフだけで112個もある。
しかし一応この112個は同型ではないはずなので、これを順々にフィルターにかけていく。
Glist2 = map (lambda G: G.degree_iterator(), Glist)
Glist3 = map (list , Glist2)
Glist4 = filter (lambda L: L == [3,3,3,3,3,3], Glist3)
len(Glist4)
2
Glist2で次数を数えて、Glist3でそれをリストにして、Glist4で[3,3,3,3,3,3]のものを抜いて、要素数を数えると2個だったので、[3,3,3,3,3,3]のラベル無しのグラフは2種類しかないことが確認できたと思います。
うむ。このやり方では数しかわからないけど、まあ、今日はここまで。
接続行列からでもグラフがかけるか実験します。
接続行列Mで与えられるグラフを描け。
M=matrix(5,8,[[0,0,1,1,1,1,1,0],[0,1,0,1,0,0,0,1],[0,0,0,0,0,0,0,1],[1,0,1,0,1,0,1,0],[1,1,0,0,0,1,0,0]])
G=Graph(M)
show(G)
描けました。
ということは、接続行列と隣接行列(adjacent matrix)の相互変換が可能ということか。
sage: G.incidence_matrix()
[1 1 1 1 1 0 0 0]
[1 0 0 0 0 1 1 0]
[0 0 0 0 0 1 0 0]
[0 1 1 1 0 0 0 1]
[0 0 0 0 1 0 1 1]
sage: G.adjacency_matrix()
[0 1 0 3 1]
[1 0 1 0 1]
[0 1 0 0 0]
[3 0 0 0 1]
[1 1 0 1 0]
できました。便利かも。
